
在上一期的文章中,我们提到了两种参数估计法,极大似然法和最小二乘法。这两种方法也是一般最常用的参数估计方法。极大似然估计(MLE)法的根本原理是找到最大化样本出现概率的参数作为对概率分布中未知参数的估计值。这被认为是最稳健的参数估计方法之一。
为了更好的理解极大似然法,我们先来看一个简单的例子。现在假设有一个袋子里面装着若干个黑球和白球。在这个情形下未知参数为随机抽取到一个黑球的概率,也是我们想估计的参数值。我们随机抽取10个球,其结果如下:前7个是黑球和后3个白球。假设随机抽到黑球的概率为1-p,那么随机抽到白球的概率为p。那么我们可以把得到7个黑球和3个白球的概率写成关于的函数,如下:
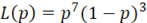
现在按照极大似然法的基本原理,我们要找p使得L(p)的值最大。那么我们可以对L(p)求导然后让导数等于0来求解最大值。

解得:
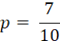
换句话说让7个黑球和3个白球这个事件出现概率最大的那个参数p为7/10。即随机抽到黑球的概率为7/10。这也于我们的直觉相符合。在这个例子中,函数L(p)被称为似然函数。但是当随机变量从离散变量变为连续随机变量时,如正态分布,指数分布,似然函数的形式和定义也会随之改变。
似然函数
当随机变量为连续变量时,极大似然法通过最大化随机变量的概率密度函数来达到最大化样本出现概率的目的。那么同样的,我们可以先出新的似然函数的公式(当数据集不含有删失数据时):
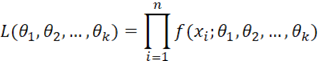
其中xi是第i个故障点的数据,θ1,θ2,…, θk是要估计的参数。其中n是完整数据集中的故障数据点数。f(xi;θ1,θ2,…, θk)是分布的概率密度函数。例如,对于双参数威布尔分布,θ1就是β,θ2就是η。为了方便计算而又不改变结果,我们一般取L的对数:

我们一般称函数K(θ1,θ2,…, θk)为评分函数(Score Function)。接着通过取偏导数找到函数K(θ1,θ2,…, θk)的最大值所对应的参数值。因为在取最大值的时候,函数的偏导数一定为零。那么我们可以把问题转化为求解下面的偏微分方程组,并把解得的参数值作为极大似然法对未知参数的估计值:
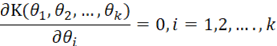
如果偏导数方程组有封闭形式的解,求解的过程会相对容易一些。如果没有封闭形式,那么我们需要使用数值求解的方法来求出参数值。
例子
现在我们来看一组数据,下面这个表格记录了完整的失效数据。我们假设它服从双参数威布尔分布(β,η),我们想用极大似然法估计这两个参数。

首先,我们得到似然函数和评分函数,K(β,η)其中f(ti ; β,η)是双参数威布尔分布的概率密度函数:

通过MATLAB我们可以画出K(β,η)的图像,如下所示:

曲面的最高点所对应的坐标就是极大似然给出的参数估计值,通过MATLAB里的max函数,我们得到曲面的最高点为K(1.79,43.27)=-26.6413。同样的我们可以用国可工软得到相近的结果。
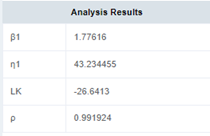
其中LK值就是曲面最高点所对应的值。
处理右删失数据
现实情况中,故障测试数据通常会包含右删失数据。这时候我们需要改变一下似然函数的公式。对于右删失数据,我们需要连续随机变量的累积密度函数(cdf)。这个新的似然函数的形式为:
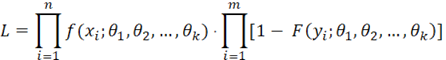
其中m是右删失数据点的数量,yi是第i个右删失数据点,而F(yi;θ1,θ2,…, θk)是分布的累积函数。对于含有右删失数据点的数据集,我们在做极大似然估计的时候使用新的似然函数,但之后的分析过程与处理完整数据一样:取似然函数的自然对数,取参数的偏导数并找到最大值。
极大似然估计在处理包含右删失数据的数据集的时候相对于其他参数估计方法有一些优势。首先,如前面的公式所示,极大似然估计考虑了右删失的数据点。概率绘图法和最小二乘法仅考虑右删失数据的相对位置,而不考虑实际的右删失数据点的值。这使得极大似然估计在处理含有大量右删失的数据集时有着较好的表现。极大似然估计的第二个优点是它理论上可以对含有右删失数据的数据集进行参数估计。虽然偏导数求解最大值的方法使得极大似然估计无法求解有多个参数而且只含有右删失数据的数据集。对于这种情况,要么使用单参数分布,要么假设分布中一些参数的值。
极大似然估计仅使用故障时间或右删失数据进行分析,没有任何对可靠性/不可靠性数值或估计值的计算。这有时会导致最后拟合得到的模型(曲线)无法经过所有的概率图上绘制的数据点。但这并不意味着极大似然估计的方法是“错误的”或者“不准确的”。
极大似然估计的优缺点
极大似然估计法有很多很好的统计性质。比如当样本量足够大的时候,它是一个无偏估计(unbiased estimator)。这意味着,估计的参数值也符合正态分布。还有当样本量增大时,极大似然法的参数估计值会收敛到参数的真实值。这两种性质都是非常好的统计性质。前一种,我们称它为渐进一致的,后一种我们称它为渐近有效的。但是极大似然法应用在实际情况中时也有它的缺陷,比如达到所需的样本量可能会非常大。有时候需要三十到五十,甚至一百多个的精确失效数据才能使参数的估计值收敛到真实值。当数据不够多的时候,最大似然估计法不再是无偏估计。比如,极大似然对威布尔分布中的参数估计,当样本量较小时是有偏估计。并且这种偏差会根据右删失数据量的增加而增加,进而致使分析结果出现差异。
极大似然估计法的渐近特性也有不适用的时候。其中之一就是在估计三参数威布尔分布中的位置参数时。如果形状参数的值接近1,那么极大似然估计将不再具有渐进特性。这些问题也可能导致分析结果不够理想。因此,在样本量较小且没有大量删失数据的情况下用最小二乘法进行估计会比较好一些。但如果数据量较多但包含分布不均的删失数据,或者当样本量足够大时,极大似然估计法会表现的更好。
参考文献



