一、两位大伽

帕斯卡(Blaise Pascal,1623~1662)是法国数学家、物理学家、哲学家、散文家。1623年6月19日生于克莱蒙费朗;1662年8月19日卒于巴黎。
帕斯卡4岁丧母,其父是政府的官吏,博学多才,是一个业余数学家。由于帕斯卡从小体弱多病,其父不让他过早接触数学,以免思虑过度有损健康。帕斯卡12岁时,看到父亲阅读几何,便问几何学是什么,父亲为了不想让他知道得太多,就简单地告诉他几何是研究图形的,并且很快把数学书收藏起来,怕帕斯卡去翻阅,父亲对他接触数学的“禁令”,更激起了帕斯卡对数学的好奇心。于是帕斯卡就自行研究,当他把自己的发现:“任何三角形的三个内角和都是一百八十度”的结果告诉父亲时,父亲惊喜交集地流出了激动的眼泪,并改变了原来的想法,提早让帕斯卡学习《几何原本》等经典数学名著。帕斯卡贪婪地很快读完了《几何原本》。
1653年他写成了《论算术三角形》,经费马修订后于1665年出版,在这本书中建立起概率论的基本原理和有关组合论的某些定理。并与费马共同建立了概率论和组合论的基础,给出了关于概率论问题的系列解法。莱布尼茨后来读到帕斯卡这方面的研究成果时,深刻地意识到这门“新逻辑学”的重要性。
帕斯卡认为:“一个人的美德决不能从他特别的努力来测度,而应该从他每天的行为来测度”。他还说:“你要人们赞美你吗?那么你不要称赞你自己”。他认为:“数学是对精神的最高锻炼”。
帕斯卡在早年就表现出了超常的数学能力,是一位在科学史上富有传奇色彩的人物,18世纪的大数学家达朗贝尔(D’Alembert,1717~1783)赞誉他的成就是“阿基米德与牛顿两者工作的中间环节”。在数学史中他被称作“最伟大的天才”(Greatest Might-Have-Been),他曾经对微积分、射影几何、概率论等数学分支做出了巨大的贡献。他拥有如此高的数学天赋和非常敏锐的直觉能力,他理应创造更多的发现。不幸的是,在他生命的大部分时间里,他倍受敏感性神经痛和精神幻觉症的折磨。他于1662年去世时年仅39岁。

费马(Pierre de Fermat,1601~1665)是法国数学家。1601年8月20日(另一说17日)生于图卢斯附近的波蒙特;1665年1月12日卒于卡斯特尔。
费马出生于皮革商人家庭,他在家乡上完中学后,考入了图卢斯大学,1631年获奥尔良大学民法学士学位,毕业后任律师,并担任过图卢斯议会议员。虽然数学只是他的业余爱好,但他对解析几何、微积分、数论、概率论都作出了杰出的贡献,被誉为“业余数学家之王”。费马在1654年写的一批信件中,他还同帕斯卡共同建立了概率论的一些基本概念。
费马性情谦抑,好静好癖。他对数学的许多研究成果都不愿发表(他的儿子在他去世后,才将其著作、信件、注记汇集成书出版)。这不但使他当时的成就无缘扬名于世,并在他的暮年也脱离了数学研究的主流,所以直到18世纪费马还不太知名。然而进入19世纪中叶,随着数论的兴起,数学家和数学史家对费马及其著作产生了浓厚的兴趣,争先发表研究费马的著作,其中尤以查尔斯·亨利(Cherles Henry)和保罗·坦纳(Paul Tannery)的4卷论文集最为全面,从中可以看出费马对数学和光学所作出的广泛而杰出的贡献。美国数学史家贝尔(Bell)说:“费马是一个第一流的数学家,一个无可指责的诚实人,一个历史上无与伦比的数论学家”。在数学中以他的名字命名的有:费马大定理、费马小定理、费马数、费马原理、费马螺线等。
二、百年未解的”点数问题”
尽管有卡尔达诺和伽利略等先驱者的一些非常重要的工作,而概率论历史学家大多赞同这样一个观点:对于数学中一个非常特别的问题的解法的探求成为数学化的概率科学产生的标志之一,这个问题被称作“点数问题”。所谓“点数问题”是指当游戏在完成前被终止时,怎样处理两名技能相当的游戏者的赌金分配问题,其依据是游戏者的得分数或是游戏终止时的点数。

意大利的帕乔里早在1494年出版的《算术、几何、比与比例集成》(Summa de Arithmetica)一书中,就提到了赌博中常常遇到的“点数问题”,他是最早在数学著作中提到点数问题的作者。紧接着,卡尔达诺和他的对手塔尔塔利亚都讨论过这个问题。然而,所有这些人,对这一问题得出的结论都不正确。直到一百多年后,在1654年,一个名为德·梅雷(de Mere,1607~1684)的法国人把这个问题寄给了当时的数学天才帕斯卡,从此概率论历史上一个决定性的阶段才开始了。
三、徳•梅雷的问题
德·梅雷是一位军人、语言学家、古典学者,同时也是一个有能力、有经验的赌徒,他经常玩骰子和纸牌。虽然他不是一个全职的数学家,但他经常从数学的角度提出和思考赌博中出现的一些有深度的问题,“点数问题”就是其中之一。这一次,德·梅雷的问题的形式是:假设两个赌博者(德·梅雷和他的一个朋友保罗)每人出30个金币,两人各自选取一个点数,谁选择的点数首先被掷出3次,谁就赢得全部的赌注。在游戏进行了一会儿后,德·梅雷选择的点数“5”出现了2次,而保罗选择的点数“3”只出现了一次。这时候,德·梅雷由于一个紧急事情必须离开,游戏不得不停止。他们该如何分配赌桌上的60个金币的赌注呢?保罗认为,既然掷出他选择的点数的机会是德·梅雷的一半,那么他该拿到德·梅雷所得的一半,即他拿20个金币,德·梅雷拿40个金币。然而德·梅雷争执到:再掷一次骰子,对他来说最糟糕的事是他将失去他的优势,游戏是平局,每人都得到相等的30个金币;但如果掷出的是“5”,他就赢了,并可拿走全部的60个金币。在下一次掷骰子之前,他实际上已经拥有了30个金币,他还有50%的机会赢得另外30个金币,所以,他应分得45个金币。
到底谁的分法对呢?当时可使两位费了不少脑筋,历史上古典概率正是由研究诸如此类的赌博游戏中的问题引起的。现在我们一起来求解,显然,为确保能分出胜负,最多需要再赛两局,为简单计,用“+”表示“德·梅雷胜”,用“-”表示“保罗胜”,于是这两局的所有可能结果为
(+,+),(+,−),(−,+),(−,−),
其中使德·梅雷获胜(即至少有一个“+”的情形)有3种,而使保罗获胜(至少有两个“-”的情形)有一种,故德·梅雷获胜的概率为3/4,保罗胜的概率为1/4。这样,德·梅雷应得全部赌金的3/4,而保罗则应得1/4,这就告诉我们,德·梅雷的分法是对的,计算机上的模拟试验也证实了这一点。
他们对这一问题的看法和计算方法不一致,为此而争论不休。后来德·梅雷把这个问题告诉了帕斯卡,帕斯卡对此也很感兴趣,又写信告诉了费马。于是在这两位伟大的法国数学家之间开始了具有划时代意义的通信(帕斯卡最初写给费马的信已不幸丢失)。在通信中,两人用不同的方法正确地解决了这个问题。
有可能结果为
(+,+),(+,−),(−,+),(−,−),
其中使德·梅雷获胜(即至少有一个“+”的情形)有3种,而使保罗获胜(至少有两个“-”的情形)有一种,故德·梅雷获胜的概率为3/4,保罗胜的概率为1/4。这样,德·梅雷应得全部赌金的3/4,而保罗则应得1/4,这就告诉我们,德·梅雷的分法是对的,计算机上的模拟试验也证实了这一点。
他们对这一问题的看法和计算方法不一致,为此而争论不休。后来德·梅雷把这个问题告诉了帕斯卡,帕斯卡对此也很感兴趣,又写信告诉了费马。于是在这两位伟大的法国数学家之间开始了具有划时代意义的通信(帕斯卡最初写给费马的信已不幸丢失)。在通信中,两人用不同的方法正确地解决了这个问题。
下面是费马写给帕斯卡的信(1654):
“先生:
如果两人赌博时以掷8次骰子为一局,而在下赌注之后我与对方商定,我放弃掷第一次的机会,那么根据我的理论应该得到全部赌金的1/6作为补偿。
如果我继续放弃掷第二次的机会,就应得到所剩赌金的1/6,即全部赌金的5/36作为补偿。
如果第三次轮到我的时候,我仍然弃权,应该得到上次所剩赌金的1/6,即全部赌金的25/216作为补偿。
如果我第四次弃权,就应得到第三次所剩赌金的1/6,即全部赌金的125/1296,您说这就是假定掷了前3次之后第四次掷的价值,我完全同意。
但您在来信的最后一个例子中说,如果我在赌博时(以掷8次为一局)要的是6点,而连掷3次都没有得到这个点数。对手建议我不掷第四次,那我就该得到全部赌金的125/1296作为补偿。按照我的理论,并非如此。因为在这种情况下,先前掷的3次什么也没得到,赌金总数未变,持有骰子而放弃第四次的人应得全部赌金的1/6作为补偿。
如果他已掷4次而没有发现期望的点数,双方商定他不再掷第五次,他依然应得全部赌金的1/6,因为赌金总数依然如故。不管是从理论上还是从常识上来说,掷每一次的价值应该是等价的。
我急于知道,您是否同意我的理论,请来信赐教。我相信我们会取得一致的意见,或者仅仅在它的应用方面有些异议。
顺致衷心祝福。
费马1654”
四、帕斯卡的回信
在1654年7月29日,帕斯卡写给费马的信中,他提到了这个问题和可能的解决方法,“你的解法非常正确,是给我印象最深的一个,但这些组合太过麻烦。我发现了另一种更为简洁的实在可行的解法”。他在信中写到:
“1.我与你的急切心情是一样的,虽然还卧病在床,但抑制不住要告诉你,我昨晚上从卡尔卡维手里接到了您关于点数问题的来信,我简直不知道用什么语言称赞这封信。我无暇详述,但可用一句话来概括,就是你已发现了如何在两个掷骰子的赌徒之间分配赌徒之间分配赌金的完善方法。看了你那令人信服的论述,我不再怀疑我犯了一个错误。对这一收获,我感到十分满意。
我认为。你关于点数问题的论述比关于骰子问题的论述更值得称赞。我已见过梅雷和罗贝瓦尔等几位先生关于骰子的问题的解答,是梅雷先生向我提起这一问题的。但是他从未发现点数问题的真正价值,也没有找到推导的方法,所以我认为我是唯一知道这种比例的人。
2.您的方法是正确的,而且是我所知道这类问题研究中的首次正确答案。但由于在组合方面会遇到过多的麻烦,我找到另一种更加简洁的方法。我乐于在这里向你作一简单的介绍,因为我很希望在我们今后的讨论中开诚布公。若能取得一致意见,那将是十分愉快的事。我清楚地看到,无论在图卢斯还是在巴黎,真理都是唯一的。
下面给出在两个赌徒之间分配赌金的方法。例如没人放32枚金币作为赌金,并以先得3分为赢。
假设第一个人已得2分,另一个人只有1分。他们掷下一次时,若第一个人赢了,她将得到全部64枚金币;若另一个人赢了,他们的比分是2:2。如果在这种情况下分赌金的话,每人将拿回自己所下的赌金既32枚金币。
综上所述,第一个人如果赢了,64枚金币将属于他;如果输了,32枚金币将属于他。假如他们将不希望继续玩下去而要分赌金的话,我一个人应该说:‘我一定能得到32枚金币即使我下一轮输了,也应该把它们给我。至于另外的32枚金币,也许你得到他们也许我得到他们,机会是均等的,所以,在给我32枚金币后,再让我们均分另外的32枚吧。’这样,她将得到48枚金币,而另一个人只能得到16枚。
现在假定第一个人得两分而另一个人得0分,他们正在争夺下一分。如果第一个人赢了,他将得到全部64枚金币。如果另一个人赢了,注意他们将回到前面的情况,即第一个人有2分而另一个人有1分。
但我们已说明了在这种情况下已有2分的人将得到48枚金币。所以,如果他们不希望继续赌下去的话,这人应该说:“如果我赢了,我将得到全部64枚金币;如果我输了,48枚金币将属于我。所以,请先把48枚金币给我,然后再均分这剩下的16枚金币,因为你我赢得它的机会是均等的”。
于是,他获得金币的数目为
48枚+8枚=56枚.
如果假定第一个人有1分而另一个人为0分。先生请看,如果他们再掷一次而第一个人赢了,他与对手的比分将是2比0。根据前述理由,56枚金币将属于他。如果他输了,他们的比分就成为1比1,32枚金币将属于他。所以他应该说:‘如果你不打算赌下去,就请把我原来的32枚金币给我,再让我们把56枚金币的剩余部分均分。56减去32为24,让我们来平分这24枚金币吧。你拿12枚我拿12枚,再加上我原来的32枚,我一共应得44枚金币”。
请看,在这种情况下,通过简单的减法,就可以知道如果他赢了第一轮,他将从对方得到12枚金币;如果他继续赢得第二轮,将再从对方得到12枚金币;赢得第三轮则得到8枚金币。
当然,我们还是别把这个问题搞得太神秘了,因为您总是希望问题明朗化的。实际上,我的目的是讨论下述观点的正确性;玩两轮的末轮价值(指从对手赌金中所得数目)是玩三轮的末轮价值的2倍,是玩四轮的末轮价值的4倍,是玩五轮的末轮价值的8倍,等。
3.但是掷末次之前的各次价值的比例就不容易发现了。我考虑了各种情况,终于找到了解决这类问题的方法。我想毫不掩饰地告诉您:当某人赢了第一轮后,不管他希望再掷多少次,都可发现掷第一次的价值。
例如,双方约定再掷8次。前8个偶数和前8个奇数为
2,4,6,8,10,12,14,16和1,3,5,7,9,11,13,15,
用下述方法乘偶数:第一个乘第二个,它们的积乘第三个,再乘第四个、第五个,依此类推。用同样的方法乘奇数:第一个乘第二个,它们的积乘第三个,等。
4.对于任意几个字母,如8个:
A,B,C,D,E,F,G,H
您可以求出从8个字母中每次取4个的组合数,以及每次取5个字母、6个字母、7个字母、8个字母的组合数。这样将得到所有可能的组合。如果您把每次取4个字母的组合数的一半与更高的组合数相加,其和将等于以2为首项,以4为公比的等比级数的第四项,项数4恰为8的一半。
作为例子,我可用拉丁字母或别的字母表示,因为法文并没什么特别的好处。
例如对任意给定的8个字母
A,B,C,D,E,F,G,H。
求出它们的所有组合数——每次取4个,取5个,直到取8个。每次取4个的组合数的一半为35(70的一半),把它与每次取5个字母的组合数(56)相加,再与每次取7个字母的组合数(8)相加,最后与每次取8个字母的组合数(1)相加,其和等于以2为首项、以4为公比的等比级数的第4项。项数4为8的一半。
以2为首项、以4为公比的等比级数的各项为2,8,32,128,512等。
在这个级数中,第一项是2,第二项是8,第三项是32,第四项是128。128显然等于
35(每次取4个字母的组合数的一半)
+56(每次取5个字母的组合数)
+28(每次取6个字母的组合数)
+8(每次取7个字母的组合数)
+1(每次取8个字母的组合数)。
5.这就是我提出的第一个定理,它纯粹是一个算术问题。关于点数问题的其他有关理论如下:
假定以5轮为一局而某人已得1分,还差4分,整个赌博的输赢将由8次掷骰子决定,而8恰是4的2倍。
如果他在得1分后,放弃掷以后各次的机会,那么他除了拿走自己所下的赌金外,还可得到对手的一部分,其分子是每次从8中取4的组合数的一半(我取4是由于它与失去的机会相等,取8是由于它是4的2倍),分母是分子与所有更高的组合数之后。
这样,如果我已得5分中的1分,对手赌金中的35/128就归我了。也就是说,如果他下128个金币的赌注,我将得到其中的35个,而把余下的93个留给他。
但是35/128分数等于105/384,后者的分母恰是从2开始的连续4个偶数之积,而分子恰是从1开始的连续4个奇数之积。
您只要略加思索,就可以毫无疑问地看清这一切,所以我认为不必再作进一步的讨论了。
6.尽管如此,我还是要把我的一个旧表寄给您,我没时间抄它。在讨论问题时,我将参考这一表格。
您将很容易地看到,第一轮的价值等于第二轮,这一方法可用组合方法证明。
您还会发现第一行的数总是增加的,第二行、第三行的数也是这样。
但在此以后,第四行的数便递减了,第五行的数也如此。这是很奇怪的。
如果双方各下256个金币的赌注,而我在第n轮都得分,对手金币中的如下数目将属于我(表1)。
表1
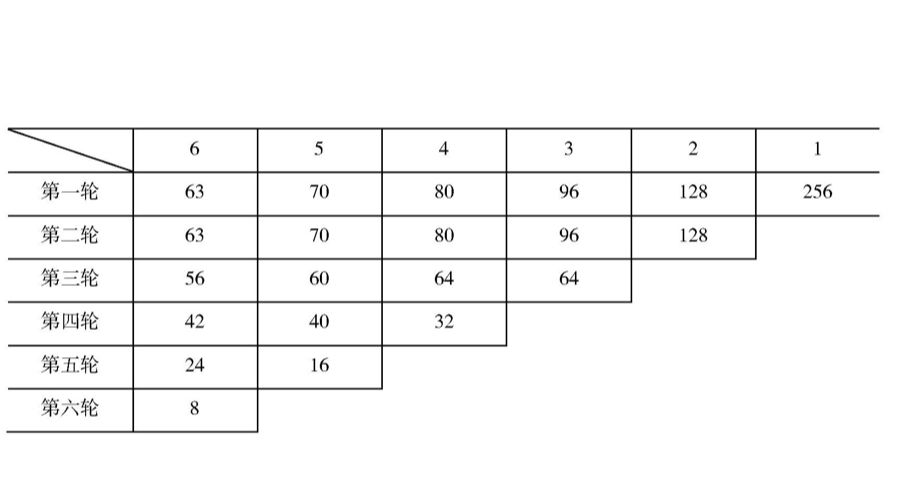
如果双方各下256个金币的赌注,而我在前n轮得分,对手金币中的如下数目将属于我(表2)。
表2
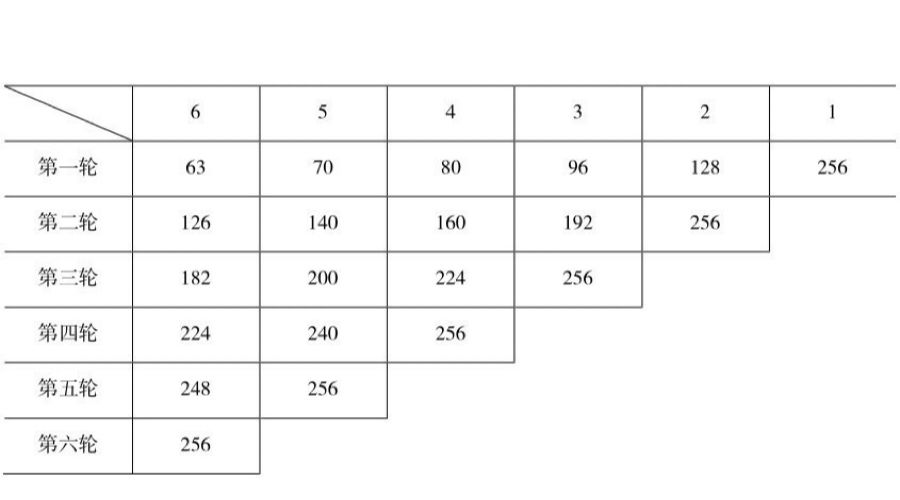
7.我没有时间在这里写出来麻烦的证明,这个证明曾使梅雷先生大吃一惊,因为他虽有才华但毕竟不是一个几何学家(您知道这是一个很大的缺陷)。他甚至连一条数学上的直线可以无限分割也不理解,他认为直线是由有限个点构成的。我一直没有改变他的看法。如果您能做到这一点,将使他变得完美一些。………
在我即将完成的一篇几何论文中,我将把上述理论条理化,我已为这篇论文下了一些功夫。
8.在这个题目下,我也作了些算术方面的工作,请不吝指教。
我首先提出一个人人可以接受的引理:从1开始的任意多个自然数所组成的连续级数(如1,2,3,4)中任何两个相邻的乘积,等于较小数与它之前各数之和的2倍。例如
4×5=2×(1+2+3+4),
这就是说没,A与小于它的各自然数之和的2倍,等于
A×(A+1).
现在给出定理:
如果从两个相邻自然数的立方差中减去1,如果等于较小数中所含各数(即从1至该数的所有自然数)之和的6倍。
令R和S是相差1的两个自然数,且S小于R,则R3−S3−1等于S中所含各数之和的6倍。
令S为A,则R=A+1,R或A+1的立方为
A3+3A2+3A+1
S或A的立方为A3,R与S的立方差为R3−S3,所以
A3+3A2+3A+1−A3=R3−S3,
两边减去单位1,得
3A2+3A=R3−S3−1.
根据引理,把A或S中所含各数之和加倍,等于A×(A+1),即
A2+A,
所以A中所含各数之和的6倍等于3A2+3A,但
3A2+3A=R3−S3−1,
所以R3-S3-1等于A或S中所含各数之和的6倍。
没有人怀疑上述证明,但人们说他们并不这样做,因为人人习惯于现成的方法。对我本人来说,把它证明出来也无利可图,只是认为应该承认这是一个很好的证明。尽管如此,我还是期待着您的不同意见。我写出证明的目的就在于此。
9.这里还有两个更困难的问题。我通过一条直线的立方与另一直线的立方相比较,证明了一个平面定理。我认为这是一个纯几何问题,而且是非常精确的,我通过这种方法解决了下述问题:‘任意给定四个平面、四个点或四个球,作一个球使之给定的球相切,经过给定的点,或经过四个平面围成的四面体的顶点。’还解决了下述问题:‘任意给定三个圆、三个点或三条直线,作一个圆使之与各圆相切,经过各点或与三条直线围成的直线外接。’
我在一个平面上仅仅用圆和直线解决了这些问题,但在证明中使用了立体轨迹——抛物线和双曲线。尽管如此,由于图形建立在平面上,我坚持认为我的解是平面解。
真对不起,我的这封常信打扰了您,使你为我的叙述花了许多时间。我想,我们之间是无话不谈的,所以把自己的见解和盘托出。但愿您能知道我的内心对你是多么的崇敬。祝我们之间的友谊不断增长。”
五、里程碑
帕斯卡和费马正确解决了“点数问题”的这一事件被伊夫斯(Howard Eves)称为“数学史上的一个里程碑”。在概率论的历史上,一般的传统观点则把这一事件看作为数学概率论的起始标志。之所以不把卡尔达诺的著作作为概率论的起源的始点,有这样几个原因:在卡尔达诺的著作中只有一小部分内容是处理机会(chance)的计算的。就像卡尔达诺的大多数作品一样,这种处理似乎只是零碎的和模糊的,混杂于卡尔达诺的个人的一些奇闻轶事、哲学思考、大量流行的赌博者常用的欺骗策略和精明的心理应用等建议之中,并且他的这本著作中所阐述的数学思想对数学家和一般的赌徒几乎都没有什么影响。因为对于当时的数学家而言,概率太游戏化了,而对赌徒而言,概率又太数学化了。而帕斯卡和费马的通信除了正确解决了一些问题和概念之外,还创造了一种研究的传统——用数学方法(主要是组合数学的方法)研究和思考机会性游戏。这种传统统治这个领域达半个多世纪的时间。所以,综合考虑所有这些因素,这个事件赢得它在数学概率论的历史中的标志性的地位是当之无愧的。本文转自: 可靠性杂坛



