一、起源于赌博

概率论起源于17世纪中叶,当时在误差、人口统计、人寿保险等范畴中,需要整理和研究大量的随机数据资料,这就孕育出一种专门研究大量随机现象的规律性的数学,但当时刺激数学家们首先思考概率论的问题,却是来自赌博者的问题。
在赌博的问题中,对后世影响最大的当数“赌本分配”(division problem)问题。所谓的赌本分配问题是这样的:两个赌徒A、B事先约定进行若干局的公平赌博(公平赌博意味着双方获胜的机会都是1/2,双方所出的赌资也都一样),直到其中一人赢了某一事先规定好了的局数为止,比方说s局。现在由于某些偶然因素导致赌博无法进行,此时A赢了s1局,B赢了s2局(s1,s2<s)。赌本分配问题最早见于意大利数学家帕乔里1494年所出版的一本书中,书名为《算术、几何、比与比例集成》。但帕乔里的推理没有包含任何的概率的理论和组合原理,因此对后世解决此问题没有任何意义。帕乔里之后,在解决这个问题上有进展的就是意大利数学家卡尔达诺。
二、卡尔达诺

卡尔达诺(Cardano Jerome,1501~1576),1501年9月24日生于意大利帕维亚(Pavia),卡尔达诺在数学方面造诣很深,特别在概率统计方面,作出了开拓性的贡献。1539年,他向著名数学家塔尔塔利亚(Tartaglia Niccolo,1500~1557)求教三次方程式的解法,并立誓予以保密。但他并没有遵守诺言,于1545年出版《代数规则大艺术》(Art Magna,简称《大术》)一书,将三次方程式公之于世。后来,三次方程式求根公式被命名为“卡尔达诺公式”,方程的解法被称为“卡尔达诺法”,而塔尔塔利亚在这方面反而湮没无闻。为了此事,卡尔达诺长期遭到学术界和舆论界的批评,被称为“不道德的人”、“剽窃者”,甚至是“臭名昭著的骗子”。不过,400多年过去后,人们开始对卡尔达诺有了重新评价,卡尔达诺在数学上并非平庸之辈,他的《大术》包含了许多他本人的独特创见,例如,他最早认识到负数和虚数,认真地加以讨论并给出了表示虚数的符号和运算法则;他对代数方程论(包括三次方程)的研究有着重要的推进,并研究了四次方程的特例。
卡尔达诺在1539年出版的一本书中开始着手解决赌本分配问题。他首先意识到,公平地分配赌本原则只与双方为获胜所需赢得局数a=s−s1,b=s−s2有关。为此他引进了一个新的赌博游戏,双方从零开始,每局双方获胜的概率相同。如果A在B赢得b局之前赢得a局,则A获胜,反之亦然。他问双方如何下注赌博才算公平的?进而他认为新问题中双方的赌注比例就应是赌本分配问题中双方分配赌注的比例。他的结论是这个比例式
b(b+1)∶a(a+1)
虽然卡尔达诺的推理已包含了一些概率的踪影,但还是相当模糊的,并且他导出的分配原则也不正确。不过他引进的新赌博游戏却为后人正确求解指明了正确的方向。
卡尔达诺的一本与概率论发展有关的著作,书名为《游戏机遇的学说》。他的《游戏机遇的学说》一书最早探讨了有关机遇的数学理论。这一著作大约完成于1564年,是他根据多年的赌博经验和数学理论写成的,主要内容是作者关于赌博中的道德情操、赌博实践、赌博理论的总结,费洛伦斯·戴维把它叫做是“理论数学家和赌徒的结合体”。
这部著作直到1663年才收入在莱顿出版的10卷本卡尔达诺《全集》(Opera omnia)中第一次发表。书中给出一些概率论的基本概念和定理,得到所谓“幂定理”(某事件重复n次发生的概率)和大数定律。但这些理论发表得较晚,对后世影响不大。
卡尔达诺于1576年9月21日在罗马逝世,享年75岁。他的一生既有着辉煌成就又历尽沧桑,饱受世人责骂和侮辱,可以说集毁誉于一生。
三、卡尔达诺的贡献
1.卡尔达诺首先申明骰子必须是“公正的”,这样作为立方体的6面骰在掷时任何一面向上的机会均等。
在书中,卡尔达诺谈到了掷距骨(踝骨)和骰子的机遇问题,通过理论上的论据提出了系统的概率计算。他说:踝骨有四面并有四个点子。但骰子有六面,抛掷六次,每个点子会出现一次。但因为有的点子出现不止一次,因而有的点子就出现不了。踝骨呈现扁平面,它的每一面位于背面之上。它不具备骰子的形式。骰子各面的总数之半总是出现相等次数,因而某个给定的点子抛掷三次的机会是均等的,因为总的变化是完全按六面顺序的。再者,在一次抛掷中,三个给定点子中之一将会出现。卡尔达诺由此推论,如果骰子不假,即如果每一面可以给予相等的权数,则我们可以计算机遇。书中明确指出,如果骰子是可靠地(honest),则六个面出现的机会相等,并且他还把“机会”(chance)定义为有利场合数与所有等可能的结果数之比。卡尔达诺的结论无疑是正确的。一颗六面完全相等的不假的骰子,每一面出现的机会,是可以通过数学抽象作出概率计算的,他还实际地计算了掷两颗或三颗骰子时在一切可能方法中有多少方法可以得到某一总点数。
2.卡尔达诺还已知并使用了概率计算中的乘法原理,这是他书中最先进的结果。
该书还利用加法原则讨论了掷两枚或三枚骰子出现的可能性问题(表1)。
表1
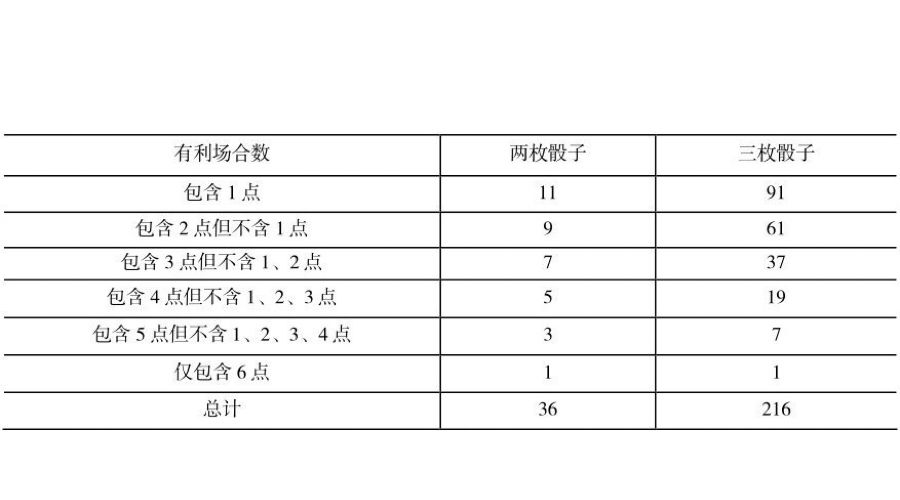
除了利用加法原则计算有利场合数外,卡尔达诺的另外一个领先于时代的结果是利用乘法原则发现了重复赌博中的赔率。作为一个职业赌徒,卡尔达诺当然更习惯用“赔率”(odds)一词来代替“机遇”(chance)或“概率”(实际上,无论是在古代还是在现代,人们在赌博时都更习惯用赔率代替概率)。赔率这个词对于喜欢参与足球博彩的人来说是再熟悉不过了。赔率与概率的关系可以用一个简单的例子来说明:比方说,如果阿根廷夺取世界杯的赔率是1:5或1赔5,那么阿根廷夺取世界杯的概率就是1/(1+5)=1/6。
卡尔达诺考虑了如下情况:设一局赌博中所有可能结果数为t,有利结果数为r,则赔率为r:(t−r)。问题是重复地进行n局这样的赌博,赔率是多少(也就是n局全部获胜才算获胜的赔率)?经过反复摸索,卡尔达诺终于发现正确的答案是
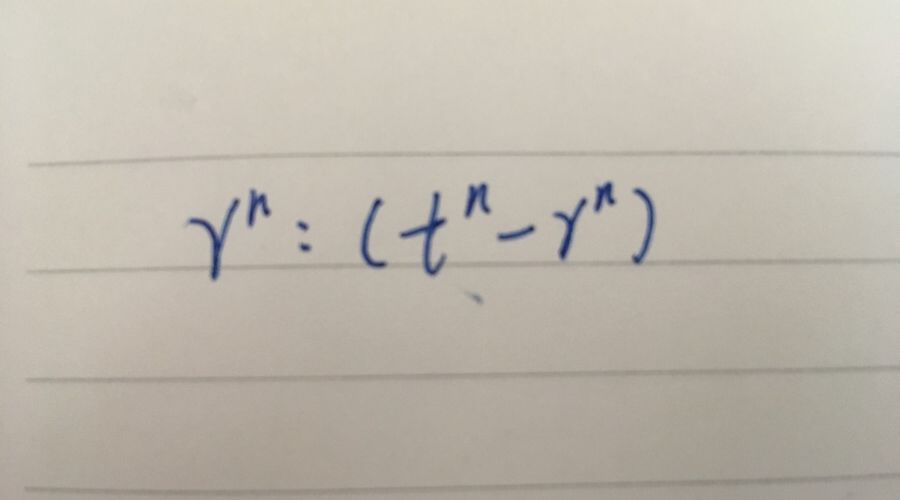
令p=r/t,则上面问题的现代表述方法
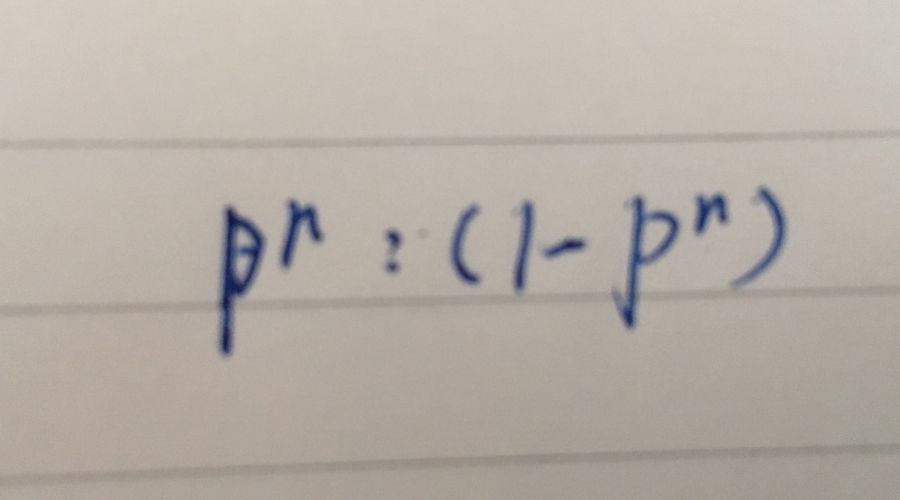
卡尔达诺除了上述对概率论的贡献外,他还在1570年导出组合公式
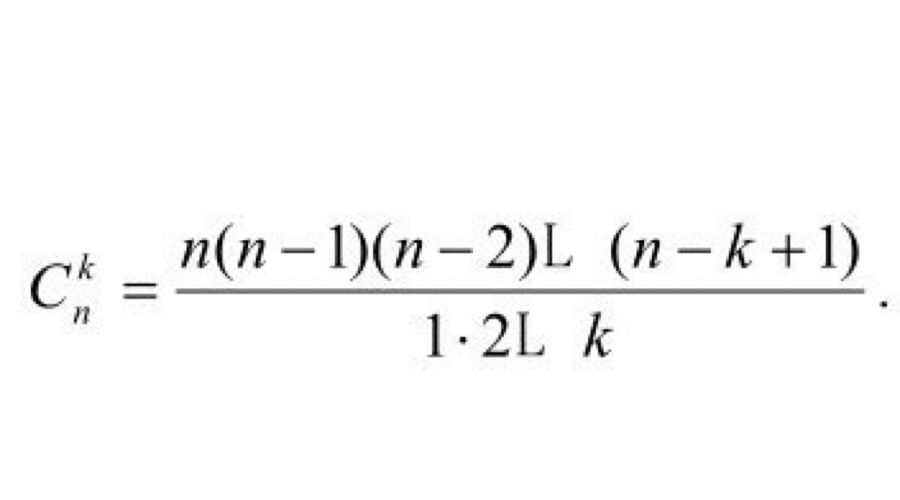
3.利用平均值法则进行计算。对于6面骰,各面的点数之和为21,被6除后得3.5,即每一掷的平均得点数为3.5。当三个骰子一起掷时,最大点数是18,最小点数是3,和为21,则平均数是10.5。
卡尔达诺重点分析了距骨游戏中的平均值计算。距骨骰的4个面分别是1,6,3,4点。1被认为是不幸运而6则表示幸运。这种游戏常常是4个骰一起掷。其点数的组合只有35种情形,而排列则有256种。出现1,3,4,6情形称为维纳斯(Venus),共有24种排列,出现的概率约为1/11。4个距骨的最大点数是24,最小点数是4,和为28,则平均值为14。这样,同时掷4个骰时,只要有多于一点出现(即至少两个一点),这一掷就是不利的。因为其他两个骰无论是什么数,这一掷都不能超过平均数。人们掌握了平均数法则,再了解前述的可能情形计算,就可以在游戏赌博中掌握一定的主动权,从而选择有利的下注方式。
四、伽利略的贡献

伽利略(Galileo,1564~1642)在早期概率发展史上也占有一席之地。在1610年前后,为了回答佛罗伦萨宫廷贵族的赌博问题,他写了短文《关于骰子游戏的思想》,解决了以下问题:同时掷三个骰子,点数和为9的情形有6种(1,2,6)、(1,3,5)、(1,4,4)、(2,2,5)、(2,3,4)和(3,3,3)。点数和为10的情形也有6种(1,3,6)、(1,4,5)、(2,2,6)、(2,3,5)、(2,4,5)、(3,3,4),那么出现点数和为9与10的机会应相同,而经验告知,出现10的机会比出现9的机会要多,原因何在?伽利略利用列举法得出了三个骰子的所有和数的不同,指出出现点数和为9和12有25种不同掷法,而出现点数和为10和11有27种,从而解释了为什么后者更容易出现的原因。伽利略也直觉地使用了等可能的思想,可见,已经产生了概率论的某些萌芽。
五、结束语

卡尔达诺是将数学理论应用于赌博游戏研究的先驱之一。在他之前这种研究只有零星结果,例如掷三个骰子有56种组合方式发现于10世纪,有216种排列方式发现于13世纪。但卡尔达诺是第一个系统论述掷骰游戏的数学家。他用数学语言将所谓运气、机遇等经验公式化,创立掷距骨游戏中的各种概率大小。首次论述纸牌游戏中某些抽签的概率,还具体计算连续二次或三次掷两个或三个骰子的得点方法,并指出这种方法适用于任意次掷骰,是概率中“大数定律”的雏形,他不仅懂得如何实际参与赌博游戏获利,而且善于总结理论规律以指导实践,这在当时是罕见的。
卡尔达诺对掷骰问题所作的概率研究和计算,早于帕斯卡和费马建立概率论100多年,表明他是概率论的创始者。
本文转自: 可靠性杂坛



